Vous pouvez télécharger ce cours au format pdf : Télécharger
Chapitre 2
Etude du phénomène de glissement en phase accélération
On démontre que la position du centre de gravité et l’adhérence au sol des roues motrices permettent de calculer une accélération limite à ne pas dépasser (sous peine de dérapage ou weeling)
On traite successivement les 2 cas:
->robot avec essieu moteur décalé
->robot avec essieu central et symétrie centrale
weeling: phénomène bien connu en moto qui consiste à décoller la roue avant à l’accélération, ou la roue arrière au freinage)
Répartition des appuis
(Robot avec 2 roues arrière et 2 billes à l’avant)
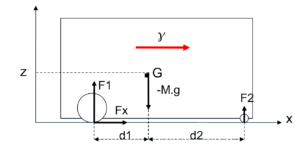
F1 et F2 représentent les réactions du sol sur la roue motrice et sur la bille de soutien.
-M.g représente la force de pesanteur appliquée au centre de gravité.
On pose d= d1+d2
Les relations générales de la mécanique donnent pour le système en équilibre:
2.F1 + 2.F2 – M.g=0 (somme des forces verticales =0) 2.Fx=M. γ( somme des forces horizontales= M. γ) F2.d2 – F1.d1 + FX.z=0(somme des couples appliqués au point G =0)
On en tire:
(2F1)/M.g = d2/d + (γ/g).(z/d) (2F1)/M.g représente la répartition des masses sur l’essieu moteur
(2F2)/M.g = d1/d – (γ/g).(z/d) (2F2)/M.g représente la répartition des masses sur l’avant
Les termes d2/d et d1/d représente les répartitions des masses en statique. (lorsque γ=0)
On voit apparaître le terme supplémentaire (γ/g).(z/d) qui représente le transfert de masse.
En phase accélération, (γ>0) ce transfert de masse augmente l’appui arrière et déleste l’avant. En phase freinage, (γ<0) les roues motrices sont délestées.
Choix de l’accélération (Robot avec essieu arrière)
Rappel des formules:
(2F1)/M.g = d2/d + (γ/g).(z/d)
(2F2)/M.g = d1/d – (γ/g).(z/d)
2.Fx=M. γ
En phase accélération, il faut éviter: Le patinage des roues motrices : Fx< ka.F1 soit γmax1 = g. ka. d2/(d-ka.z)
Le décollage de l’avant (weeling) : F2>0 soit γ max2 = g.d1/z
On retient pour γ max la plus petite de ces 2 valeurs.
En phase freinage, il faut éviter:
Le patinage des roues motrices: |Fx|< ka.F1 soit γ max1 = g.ka.d2/(d+ka.z)
Le décollage des roues arrières(weeling): F1>0 soit γ max2 = g.d2/z
On retient pour γ max la plus petite de ces 2 valeurs. (γ max représente le max de la valeur absolue de γ )
Exemples avec ka=1
En marche AR, les résultats sont inversés
| En accélération: | Au freinage: |
| γmax1=1.2g γmax2=0.8g c’est le weeling qui limite l’accélération:γmax = 0.8g soit environ 8m/s² |
γmax1=0.4g γmax2=1.2g C’est le dérapage qui limite l’accélération γmax = 0.4g soit environ 4m/s² |
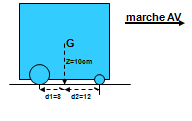
En marche AR, les résultats sont inversés
| En accélération: | Au freinage: |
| γmax1=3g γmax2=0.5g C’est le weeling qui limite l’accélération: γmax = 0.5g soit environ 5m/s² |
γmax1=0.3g γmax2=0.75g C’est le dérapage qui limite l’accélération: γmax = 0.3g soit environ 3m/s² |
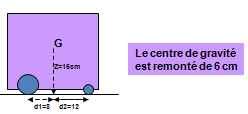
Commentaires sur le choix de l’accélération max (Robot avec essieu arrière)
On rappelle les limites de l’étude qui ne porte que sur des déplacements en translation. Ce choix permet d’optimiser l’accélération en terme de performance maximum. (On verra plus tard comment choisir les moto réducteurs capables de passer cette accélération)
A remarquer la simplicité des résultats qui ne dépendent que de la position du centre de gravité et du coefficient de frottement des roues au sol.
En particulier, le poids du robot n’intervient pas ce qui ne constituait pas une évidence à priori.
Le rappel des 2 formules,
(2F1)/M.g = d2/d + (γ /g).(z/d)
(2F2)/M.g = d1/d – (γ /g).(z/d)
conduit aux remarques suivantes:
On a intérêt à avoir le maximum d’appui sur l’essieu moteur, donc augmenter autant que possible le rapport (2F1)/M.g, soit le terme statique d2/d, ce qui conduit à positionner le centre de gravité au plus près de la verticale de l’essieu.
Quand au transfert de masse dynamique (γ /g).(z/d) il change de signe avec γ, ce
qui donne de l’appui aux roues motrices pendant l’accélération, mais les déleste pendant le freinage.
Comme nos robots en cours d’un match, freinent autant qu’ils accélèrent, il semble raisonnable de diminuer autant que possible ce transfert de masse qui dépend simplement du rapport (z/d), en abaissant le centre de gravité.
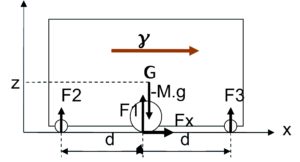
Les vecteurs F1 et –Mg sont colinéaires
(Le léger décalage sur la figure est fait pour raison de lisibilité)
On a simplifié en supposant une symétrie mécanique du robot.
En statique (γ=0) :
F2 = F3=0
2F1= Mg
Le poids du robot appuie entièrement sur l’essieu moteur
Voyons maintenant le transfert de masse dû à l’accélération: On démontre que:
Si le robot accélère (γ >0)
(2F1)/Mg = 1 – (γ /g).(z/d) à Le transfert de masse déleste l’appui sur l’essieu
(2F2)/Mg = (γ /g).(z/d à Le robot prend appui sur les billes arrières
(2F3)/Mg= 0
Si le robot freine (γ >0)
(2F1)/Mg = 1 – (γ /g).(z/d) à Le transfert de masse déleste l’appui sur l’essieu
(2F2)/Mg = 0
(2F3)/Mg= (γ /g).(z/d) à Le robot prend appui sur les billes avant
Rappel du résultat : Conclusion sur choix de l’accélération avec essieu central
Si le robot accélère (γ >0)
(2F1)/Mg = 1 – (γ /g).(z/d) Le transfert de masse déleste l’appui sur l’essieu
(2F2)/Mg = (γ /g).(z/d Le robot prend appui sur les billes arrières
(2F3)/Mg= 0
Si le robot freine (γ >0)
(2F1)/Mg = 1 – (γ /g).(z/d) Le transfert de masse déleste l’appui sur l’essieu
(2F2)/Mg = 0 Le robot prend appui sur les billes avant
(2F3)/Mg= (γ /g).(z/d)
Il y a symétrie totale entre accélération et freinage
L’appui sur l’essieu moteur diminue du même transfert de charge en accélération et freinage
Calcul de γ max:
condition de non patinage: Fx< ka.F1 ( ka: coefficient de frottement) entraîne:
γ max1/g = ka/(1+ka.z/d)
condition de non weeling: F1>0 entraîne:
γmax2/g = d/z
Montrons que le weeling est impossible avec cet essieu central symétrique:
En combinant les 2 équations, on obtient:
γmax1= γmax2 / (1+ γmax2 /ka.g) soit γmax1 < γmax2 CQFD
Exemple: d=15cm z=15cm ka=1
γ max1/g =0.5
C’est le dérapage qui impose la valeur de γ max avec
γ max=0.5g Limite valable aussi bien pour le freinage que pour l’accélération
Récapitulatif des formules de calcul de l’accélération maximum
Avec essieu décalé
a l’accélération:
γmax1 = g. ka. d2/(d-ka.z)
γ max2 = g.d1/z
au freinage
γ max1 = g.ka.d2/(d+ka.z)
γ max2 = g.d2/z
prendre pour γ max la plus petite des 2 valeurs γ max1 et γ max2
Avec essieu central et robot symétrique
γ max = g.ka/(1+ka.z/d)
Par sécurité par rapport à des fluctuations possibles de ka, se garder une marge de sécurité par rapport à cette valeur max (par exemple 0.8.γ max ).
Ces formules sont d’autant plus intéressantes qu’on a appris à mesurer ka et qu’il est possible de déterminer avec précision la position du centre de gravité c’est-à-dire les valeurs de d1, d2, d, z.
Il suffit pour cela d’utiliser la méthode du manche à balai présentée à la page suivante et qui encore une fois, fait appel à un matériel de haute technologie, soit:
à Un manche à balai ou barre ronde
à Une règle graduée
Localisation du centre de gravité

Mesure de z (hauteur de G)

Robot volontairement lesté à gauche. Mesure de la distance entre projection au sol de G et essieu

On vérifie que G est bien dans le plan médian. (Symétrie parfaite droite-gauche)
On recherche la position d’équilibre du robot en le faisant rouler sur la barre posée au sol. La position d’équilibre étant instable est maintenue délicatement par 2 doigts. On mesure la distance par rapport à la barre, avec la règle posée au sol perpendiculairement à la barre
(Si le robot est de forme cylindrique, ça doit être encore possible).
