Vous pouvez télécharger ce cours au format pdf : Télécharger
Chapitre 4
Les lois mécaniques et thermiques dans un moteur
On rappel d’abord les lois de base d’un moteur continu en régime établi.
Puis on évoque les problèmes thermiques
A ce stade, on a appris à choisir l’accélération max. Encore faut-il que nos moto réducteurs puissent fournir le couple nécessaire à ces performances.
On se limitera au choix de moteurs continus, en laissant de côté les moteurs brushless, bien
que très excitants pour leurs performances. Mais notre expérience est trop limitée sur le sujet.
Présentation du problème :
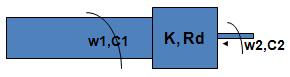
On pose:
K : le rapport de réduction du réducteur.
Rd: Rendement mécanique du réducteur
w1: vitesse angulaire moteur w2: vitesse angulaire roue
C1: couple moteur C2: couple à la roue
P1=C1.w1: puissance mécanique moteur P2=C2.w2: puissance mécanique à la roue
w2 = w1/K
C2 = C1.Rd.K
P2 = P1.Rd
Remarquer que la relation sur les puissances ne dépend pas de K.
Si on augmente K, on augmente le couple roue, mais on diminue la vitesse du robot
d’où le dilemme dans le choix de K.
Rappels de base sur le moteur continu:
U = r.i + λv.w
C = λc.i
les variables: U: tension d’induit (v) w: vitesse de rotation (rd/s) C: couple moteur (N.m) i: courant d’induit (A)
les constantes:
r: résistance d’induit (ohm)
λv: constante de vitesse (v/rd/s)
λc: constante de couple (N.m/A)
Courbes en fonction du couple moteur à tension U constante
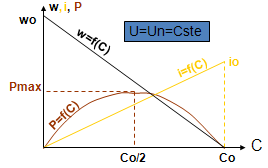
La vitesse w diminue linéairement quand le couple augmente.
Le courant d’induit i est proportionnel au couple.
wo=Un/λv (vitesse à vide pour C=0)
io=Un/r (courant de démarrage pour w=0)
Co=λc.io (couple de démarrage pour w=0)
Remarque inattendue et incroyable:
λv=λc (dans le système Si: λv en v/rd/s et λc en N.m/A)
La puissance mécanique P=C.w que peut fournir le moteur passe par un maximum pour Co/2.
A la puissance max Pmax: Le terme ri (terme ohmique ou terme de couple) est égal au terme λv.w (terme de vitesse) ce qui signifie que la moitié de la tension U sert à maintenir le couple, l’autre moitié sert à maintenir la vitesse. La puissance électrique U.i fournie au moteur est alors égale à 2.Pmax donc le rendement énergétique n’est que de 50%.
Les phénomènes thermiques dans le moteur
La puissance Pj dissipée dans le moteur élève sa température. Et la température du rotor ne doit pas dépasser une valeur limite de l’ordre de 100°C à 125°C.
Pour les types de moteurs utilisés pour Eurobot, les ordres de grandeur des paramètres qui définissent les échanges thermiques sont les suivants:
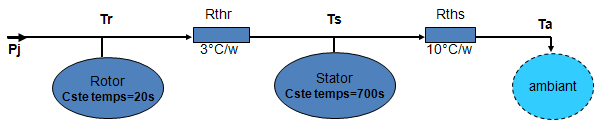
Résistance thermique rotor stator Rthr= 3°C/W
Résistance thermique stator ambiant Rths= 10°C/W
Constante de temps thermique rotor 20s
Constante de temps thermique stator 700s
Les lois d’ohm thermiques donnent en régime permanent:
Tr-Ts = Pj.Rthr Tr: température du rotor
Ts–Ta = Pj.Rths Ts: température du stator
Tr- Ta = (Rths+Rthc).Pj Ta: température ambiante
Durée de vie d’un moteur en cas de blocage de la roue
Le calcul qu’on va présenter peut être considéré comme théorique. En fait il ne l’est pas tant que ça:
On suppose un robot asservi en position, en train de se déplacer. On va provoquer brusquement un blocage d’une roue (par un procédé quelconque qui ne nous intéresse pas pour l’instant). On suppose par ailleurs que le robot est dépourvu d’un système logiciel de détection de blocage.
Essayons d’évaluer la durée de vie du moteur associé à la roue bloquée.
L’asservissement va réagir au blocage en augmentant la tension de commande jusqu’à saturation c’est-à-dire la tension d’alimentation. Par conséquent, le courant d’induit va augmenter jusqu’ à sa valeur imax.
imax=Vcc/r (On néglige la chute de tension dans le pont en H)
Pj = r.imax² puissance dissipée au rotor du moteur.
La température du stator n’a pas le temps de varier étant donné la valeur de sa constante de temps thermique (700s par exemple).
Par contre, la température du rotor va augmenter très rapidement, étant donné sa constante de temps thermique de l’ordre de 20s.
Prenons l’exemple du moteur RE025 en version 24v:
r = 2.34ohm Rthr=3°C/w cste de temps thermique rotor= 20s
Vcc=24v Trmax=110°C Ta=25°C
Imax = Vcc/r = 24/2.34 = 10.25A
Pj=r.imax² =246 w puissance dissipée au rotor
Tr- Ta = Rth.Pj =737 °C
Bien entendu il s’agit d’une valeur asymptotique qui ne sera jamais atteinte car le rotor va partir en fumée au delà de Tr=110°C, soit Tr-Ta = 85°C
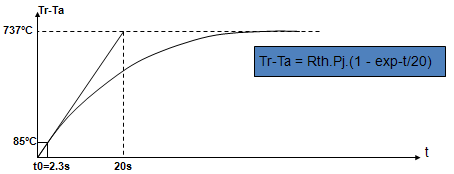
En approximant l’exponentielle avec sa tangente ça donne une durée de vie t0:
t0= 20. 85/737 = 2.3 s
La durée de vie du moteur après blocage de la roue est de 2.3 s
(A moins que l’ampli de puissance serve de fusible et lâche avant ☺)
Inquiétant n’est-ce pas.
