Vous pouvez télécharger ce cours au format pdf : Télécharger
Chapitre 6
Choix de la vitesse et de l’accélération
On va s’imposer un fonctionnement des moteurs sans saturation et en
déduire les performances du robot en terme de vitesse et accélération
Evaluation des performances sans saturation
On s’impose un fonctionnement de l’asservissement sans saturation. La tension U d’alimentation des moteurs doit par conséquent rester inférieure à tout instant à sa tension de saturation Vsat.
Dans un fonctionnement sans blocage, cherchons à quel moment la tension U va passer par son maximum.
Dans le raisonnement qui va suivre on revient au profil trapézoïdal de vitesse, en rappelant qu’il s’agit d’un profil souhaité c’est-à-dire qu’il correspond à un profil de consigne de vitesse. Afin de simplifier le problème, on supposera que ce profil correspond au profil de vitesse effective. Ce qui revient à négliger les écarts de boucle dans l’asservissement.
Fonctionnement normal du robot sans blocage
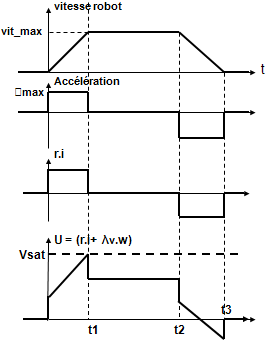
On retrouve le profil trapézoïdal de vitesse.
L’accélération du robot est constante= γ max
pendant les phases accélération et freinage.
Si l’accélération est constante, le couple moteur donc le courant sont constants.
On retrouve que U est la somme du terme ohmique et du terme de vitesse.
De 0 à t1, le terme ohmique est constant, le terme de vitesse est proportionnel à la vitesse robot.
U est maximum à l’instant t1.
Si on veut tirer la quintessence du moto réducteur, il faut choisir γ max et vit_max de façon à ce que cette valeur max de Ucorresponde à la tension de saturation Vsat.
Ce qui signifie qu’on se place en limite de saturation à l’instant t1 le plus critique.
Les limites de fonctionnement sans saturation sont donc données par l’équation:
Vcc=r.i + λv.wm (1) équation valable à l’instant t1 (en fin de phase accélération)
i= Cm/λc courant d’induit (A)
Cm=Cr/(K.Rd) couple moteur (N.m)
Cr=Fx.D/2 couple roue (N.m)
2Fx=M. γ force de traction (N)
wm =K.wr wm:vitesse angulaire moteur; wr: vitesse angulaire roue (rd/s)
v=2.wr/D vitesse linéaire du robot (m/s)
L’équation (1) devient si on exprime i en fonction de γ et wm en fonction de vmax
Vcc= [(r+ra).D.M/(4.K.Rd. λc )]. γ + [2.λv. K/D].vmax
Equation de la forme:
Vcc=a. γ + b. vmax
Equation d’une droite si on représente vmax en fonction de γ
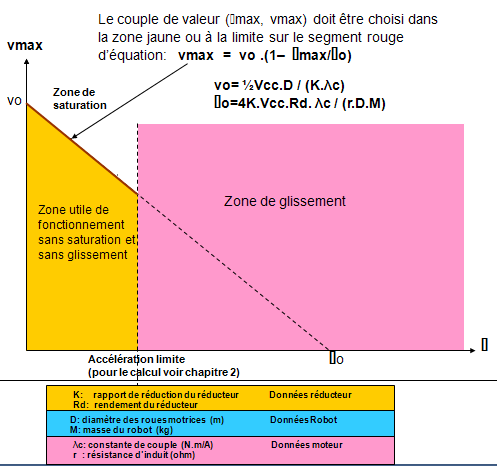
Reprenons les 2 moteurs donnés en exemple au chapitre précédent
Données robot:
M=15kg masse du robot
D= 6cm diamètre des roues
ka=1 coefficient d’adhérence
Batterie de 27v
| Moteur puissance 10w 24v
r=7.55 ohm λc=43.8 mN.m/A vitesse limite 5500tr/mn Réducteur K=36 |
Moteur puissance 20w 24v
r=2.34 ohm λc=23.5 mN.m/A vitesse limite 11000tr/mn Réducteur K=20.25 |
| L’application des formules page précédente donne: | |
| Moteur puissance 10w
vo=0.51m/s γ o=1.7g |
Moteur puissance 10w
vo=1.7m/s γ o=1.6g |
Soit les droites de fonctionnement:
Vitesse et accélération maximum pour nos 2 moto réducteurs
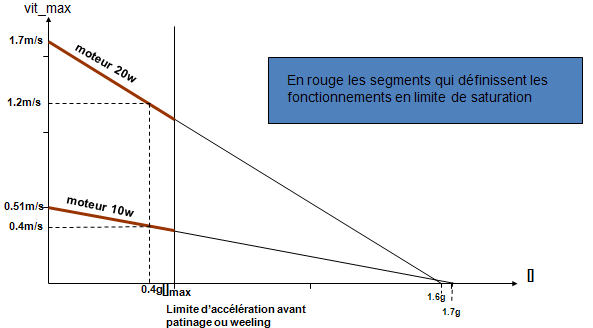
Exemple :
Si on se fixe une accélération de 0.4g:
Avec le moteur 20w, la vitesse ne doit pas dépasser 1.2m/s
Avec le moteur 10w, la vitesse ne doit pas dépasser 0.4 m/s
