Vous pouvez télécharger ce cours au format pdf : Télécharger
Chapitre 8
Asservissement
L’essentiel sur le sujet a été largement évoqué à l’occasion d’échanges à travers le forum et d’articles disponibles sur les sites d’équipes participantes.
On se contentera de reprendre certains de nos documents déjà publiés sur le sujet, d’insister sur certains points et de commenter quelques résultats expérimentaux.
Les 2 principes de l’asservissement de position d’un robot
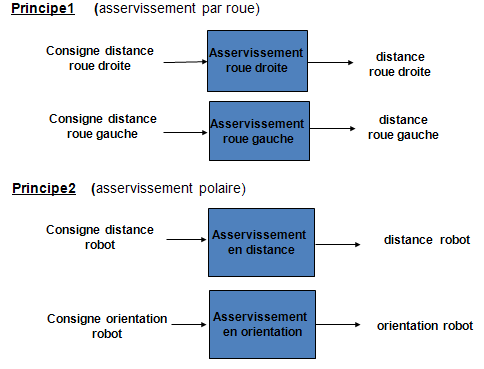
On ne revient pas sur les mérites de l’asservissement polaire, mais il faut tempérer l’idée qui consisterait à croire que ce choix est indispensable pour atteindre un bon niveau de performance.
Un robot utilisant l’asservissement de type1 bien réglé, sera toujours supérieur en performances et fiabilité à un robot en asservissement polaire mal maîtrisé.
Et il faut tenir compte du fait que des composants du genre LM629 permettent de réaliser un asservissement de type 1 clef en main, ce qui soulage le concepteur de cette tache en lui permettant de se consacrer davantage sur le reste.
A l’époque des PMI (Petits Mobiles Intelligents), autorisés par le règlement, nous utilisions cette technique avec succès. Certains anciens au passé glorieux se souviennent de PMI traversant le terrain à 2m/s ! (pas apprécié par tous☺)
De toute façon, que l’asservissement soit intégré dans un composant ou développé par logiciel, il reste un problème commun aux 2 techniques, c’est le choix des paramètres qui conditionnent l’asservissement. A savoir les gains et les seuils d’écrêtage éventuels des correcteurs PID. Il est clair q’un LM629 ne va pas inventer ces réglages et il faudra lui fournir ces valeurs.
Dans la présentation qui suit, les principes évoqués sont généraux et valables dans les 2 techniques mais les exemples sont pris en asservissement polaire.
Asservissement analogique avec correcteur PID
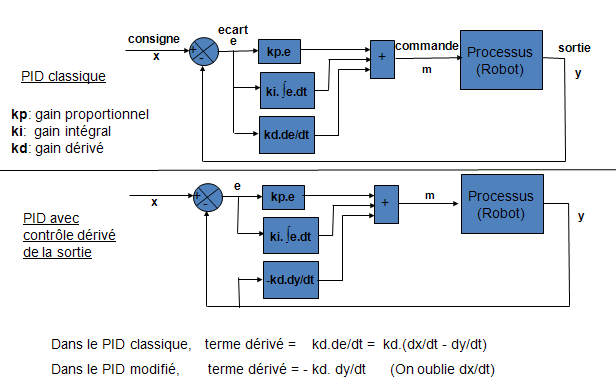
Présentons les 2 structures possibles du correcteur PID en introduisant le vocabulaire
Asservissement échantillonné avec correcteur PID numérique
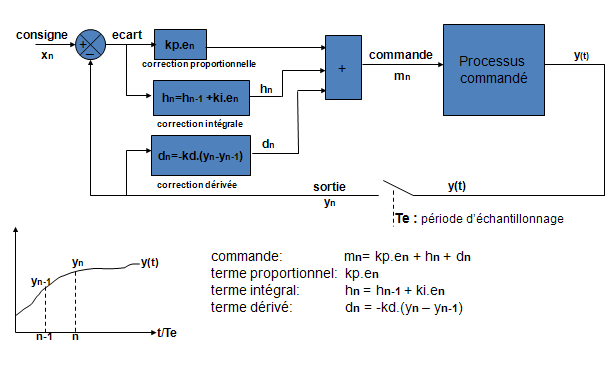
(présentation avec contrôle dérivé de la sortie)
Principe de l’asservissement polaire
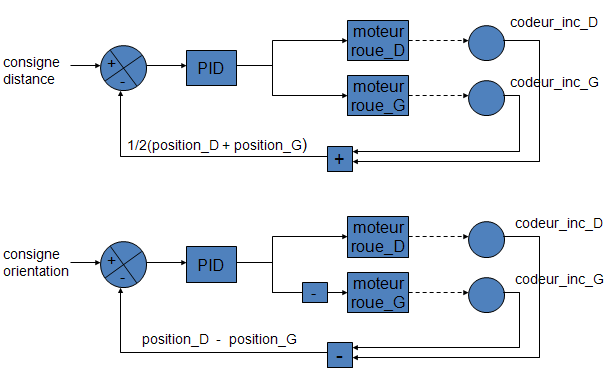
Asservissement en distance
Pour connaître la distance parcourue par le robot, on va sommer la distance effectuée par les deux roues codeuses. De cette façon, on obtient la distance parcourue par le centre de l’essieu.
L’asservissement en distance consiste à envoyer à chaque période d’échantillonnage une commande aux moteurs fonction de l’écart entre la distance réelle et la distance désirée (appelée consigne_distance)
Algorithme de l’asservissement en distance
Sans terme intégral et avec contrôle dérivé de la sortie
distance = (roue_d + roue_g) /2
vitesse= (vitesse_roue_d + vitesse_roue_g)/2
ecart = consigne_distance – distance
commande = ecart * GAIN_PROPORTIONNEL_DISTANCE
commande_distance = commande – GAIN_DERIVE_DISTANCE*vitesse
commande_roue_D= commande_distance
commande_roue_G= commande_distance
Asservissement en orientation
L’orientation du robot est obtenue par différence de la distance parcourue par les 2 roues codeuses.
A chaque période d’échantillonnage, cette orientation est comparée à la consigne orientation.
A partir de l’écart correspondant, on calcule la commande orientation qui est envoyée aux 2 moteurs (avec changement de signe sur le moteur gauche).
Algorithme de l’asservissement en orientation
orientation = roue_D – roue_G
vitesse_orientation=vitesse_roue_D – vitesse_roue_G
ecart = consigne_orientation – orientation
commande = ecart * GAIN_PROPORTIONNEL_ROTATION
commande_rotation = commande – GAIN_DERIVE_ROTATION*vitesse_orientation
commande_roue_D= commande_rotation
commande_roue_G= – commande_rotation
Algorithme complet en asservissement polaire
distance = (roue_d + roue_g) /2
vitesse= (vitesse_roue_d + vitesse_roue_g)/2
ecart = consigne_distance – distance
commande= ecart * GAIN_PROPORTIONNEL_DISTANCE
commande_distance = commande – GAIN_DERIVE_DISTANCE*vitesse
orientation = roue_D – roue_G
vitesse_orientation=vitesse_roue_D – vitesse_roue_G
ecart = consigne_orientation – orientation
commande = ecart * GAIN_PROPORTIONNEL_ROTATION
commande_rotation = commande – GAIN_DERIVE_ROTATION*vitesse_orientation
commande_roue_D= commande_distance + commande_rotation
commande_roue_G= commande_distance – commande_rotation
(Des écrêtages éventuels sont à prévoir)
Changement de système d’unité
Système d’unité SI (Système International)
Distance: d distance parcourue: (m)
Vitesse: vit: distance parcourue par seconde (m/s)
Accélération: acc: variation de vit par seconde (m/s²)
Système d’unité robot
Distance: d_rob: nombre d’impulsions codeur
Vitesse: vit_rob: nombre d’impulsions par période Te
Accélération: acc_rob: variation de vit_rob par période Te
Formules de passage
d_rob = K * d
vit_rob = (K*Te) * vit
acc_rob = (K*Te²) * acc
K=(N*Mult)/(π*D)
N: nb d’impulsion du codeur
Mult: coefficient multiplicateur (1 ou 2 ou 4)
D: Diamètre roue codeuse
Te: période d’échantillonnage
Exemple
N=1000
Mult=4 (utilisation de tous les fronts)
D=6 cm
Te=5 ms
K= 21220
K*Te = 106
K*Te²= 0.53
Reprenons l’exemple précédent
N=1000
Mult=4
D=6 cm
Te=5 ms
K= 21220
K*Te = 106
K*Te²= 0.53
d_rob = 21220*d
vit_rob = 106*vit
acc_rob= 0.53*acc
Si par exemple on veut une vitesse de 1m/s avec une accélération de 0.3g ça donne:
vit_rob = 106 soit une variation de 106 impulsions codeur pendant 5 ms
acc_rob= 0.53*3= 1.6 soit une variation de vit_rob de 1.6 pendant 5 ms
Cet exemple montre qu’il va falloir travailler en variables flottantes ce qui peut poser des problèmes de temps de calcul, à moins d’approximer 1.6 par 1 ou 2 soit une approximation de 25 % sur la valeur de l’accélération.
Une solution pour rester en variables entières est d’introduire dans le logiciel un coefficient multiplicateur sur la constante K par exemple 8. Les formules deviennent:
d_rob = 169760*d
vit_rob = 848*vit
acc_rob = 4.24*acc
Si on reprend notre exemple avec une accélération de 0.3g, ça donne:
acc_rob = 4.24*3 = 12.72 qu’on pourra approximer par 12, sans état d’âme cette fois.
Transposition des fonctions du temps
Il s’agit de transposer les fonctions du temps distance, vitesse, accélération d’un système d’unité à l’autre.
Pour passer du système SI au système robot, il suffit de remplacer t par n
Pour passer du système robot au système SI, il suffit de remplacer n par t
(n=t/Te : nombre de périodes d’échantillonnage)
Exemple: Pour les phases accélération et freinage:
Système SI
d = ½. acc.t²
v = acc.t
v2² – v1² = 2. acc.d
Système robot
d_rob = ½ . acc_rob . n²
v_rob = acc_rob . n
v_rob2² – v_rob1² =2. acc_rob . d_rob
Phase à vitesse constante
d = v . t
d_rob = v_rob . n
Quelques résultats expérimentaux
Les tests sont effectués avec le robot dans la version 12.7 kg.
La fonction utilisée pour les tests est la suivante:
tout_droit_avec_freinage(50*COEF_D, 0.8*COEF_V, 4.2*COEF_ACC);
Ce qui impose les consignes cinématiques suivantes:
distance à parcourir: 50 cm
vitesse: 0.8 m/s
accélération: 4.2 m/s²
Le correcteur d’asservissement est de type proportionnel et dérivé. (Pas de terme intégral).
L’intérêt du terme dérivé
On représente ici, l’évolution de la vitesse que l’on compare à sa consigne trapézoïdale.
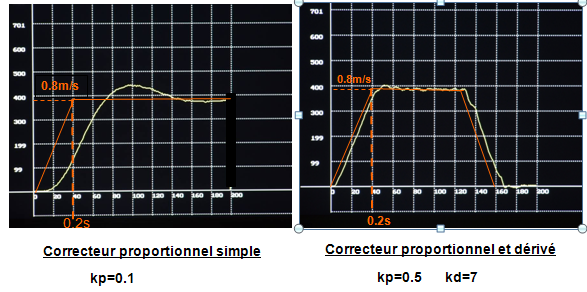
L’ intérêt du terme dérivé apparaît de façon spectaculaire.
Noter le facteur 5 sur la valeur du gain proportionnel lorsqu’on ajoute le terme dérivé.
Il faut signaler que l’échelle des temps est la même dans les 2 cas.
(La distance de déplacement a due être rallongée avec le correcteur proportionnel du fait de son temps de montée, ce qui explique qu’on ne voit pas le freinage )
Comparaison entre correcteur avec contrôle dérivé de la sortie
et correcteur proportionnel-dérivé classique.
On essaie les 2 correcteurs dans les mêmes conditions, chacun des 2 correcteurs ayant été optimisé en termes de gains proportionnel et dérivé.
Courbes de vitesse comparatives
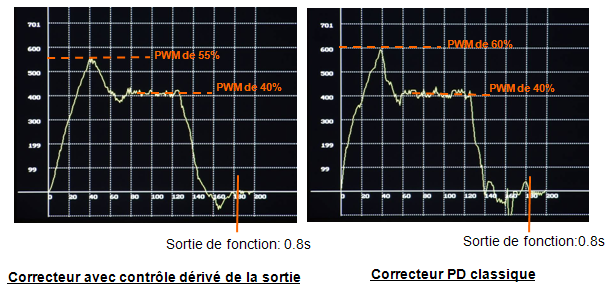
Ces courbes sont représentatives des tensions appliquées aux induits des moteurs
On retrouve le caractère plus bruité du correcteur classique. En fin de freinage ça chahute pas mal.
Le niveau de commande maximum est légèrement supérieur avec le correcteur classique.
Ce qui paraît logique car l’asservissement, plus nerveux demande plus de tension.
Courbes de distance comparatives
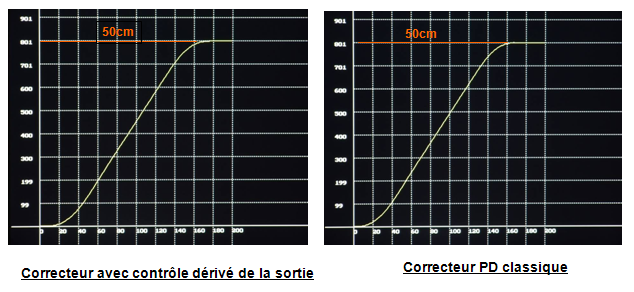
On retrouve des phases accélération et freinage un peu plus rapides avec le correcteur classique. Et pourtant la consigne accélération est la même (4.2 m/s²).
Le léger chahut en fin de freinage pour le correcteur classique n’est pas visible à cette échelle. Ca joue sur quelques mm et effectivement on perçoit un léger frémissement par observation directe du robot.
ecart= consigne_distance – distance
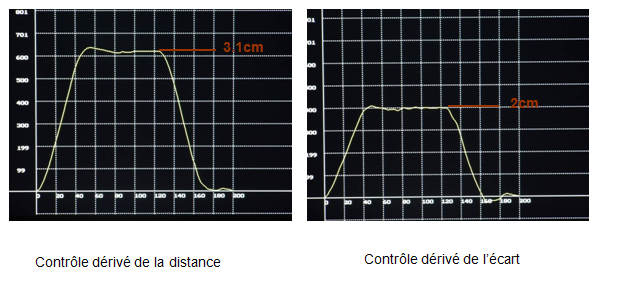
A propos du terme intégral
Tout a été dit sur le forum à ce sujet et liberté est laissée à chacun de faire son choix.
Ce qu’il faut retenir d’un point de vue théorique:
Les vertus du terme intégral:
-> améliore la précision en régime établi
-> réagit efficacement aux perturbations
A mettre au passif:
-> tendance à déstabiliser la boucle
-> introduit le phénomène de windup (largement évoqué sur le forum)
Il se trouve qu’il est très prisé par les industriels dont les processus fonctionnent plus souvent en régulateur qu’en suiveur et ses vertus face aux perturbations sont précieuses dans ces conditions.
Dans un robot EUROBOT, son emploi est plus discutable.
Vous connaissez notre point de vue sur le sujet:
à Le windup a tendance à créer des réactions brutales et incontrôlées quand cesse la perturbation. C’est vrai qu’il existe des systèmes antiwindup.
à Quand on parle de perturbations à l’Eurobot, il s’agit de blocage (adversaire ou obstacle). Et si le moto réducteur est bien choisi (voir le chapitre qui évoque le problème), le terme intégral n’apporte rien de plus.
à Quand à l’effet déstabilisant, il semble inéluctable, et un raisonnement très simple peut le démontrer:
On suppose un profil trapézoïdal pour la distance afin de simplifier la figure
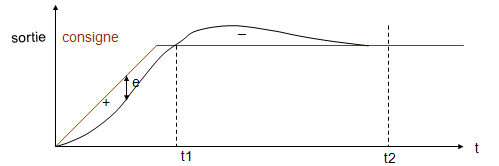
e= consigne – sortie (e: écart de boucle)
h= ki.∫ e.dt (h: terme intégral)
Supposons que l’écart s’annule en régime établi, robot à l’arrêt. (Ce qui est le cas dans un robot Eurobot.)
Si pour t>t2, l’écart de boucle est nul, le terme intégral h est nécessairement nul, sinon une tension est appliquée aux moteurs et le robot n’est pas à l’arrêt.
La valeur de h à l’instant t2 est donc nulle. Ce qui suppose que les 2 aires représentées par les signes + et – sur la figure s’annulent.
Comme de 0 à t1 la sortie est inférieure à la consigne, à partir de t1, la sortie devient supérieure à la consigne, d’où un dépassement inéluctable.
Dans beaucoup de processus industriels les dépassements ne sont pas forcément gênants, (voir recherchés). Mais dans un robot Eurobot, un dépassement en fin de freinage, signifie
que le robot va reculer. ☹
