Vous pouvez télécharger ce cours au format pdf : Télécharger
Asservissement du robot à une trajectoire
Introduction :
Comment faire bouger un robot de la Coupe suivant une trajectoire prédéfinie. L’objectif de ce document est d’aborder le problème à travers notre expérience acquise au cours de ces dernières années de participation.
Les limites de la présente étude :
Le robot se déplace sur un terrain autorisant l’odomètrie. Deux capteurs incrémentaux couplés mécaniquement à deux roues folles disposées dans l’axe des 2 roues motrices vont permettre de contrôler la trajectoire du robot. Ces codeurs sont couplés aux roues folles et non pas aux roues motrices qui peuvent glisser et par conséquent ne pas traduire fidèlement les déplacements du robot.
L’origine du robot est prise au milieu de l’essieu des roues motrices.
Asservissement de position, principe 1 :
Chaque roue folle est asservie à une consigne de position, sa position réelle étant contrôlée par le codeur incrémental associé, suivant le schéma fonctionnel suivant :
asservissement en position : principe 1
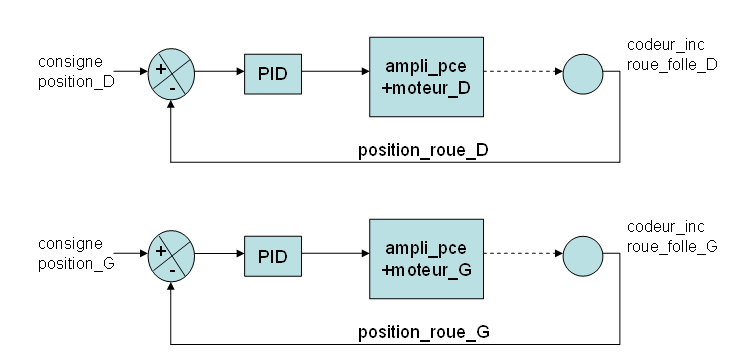
La consigne représente la valeur désirée de la position, le codeur mesurant la position réelle. L’écart entre ces 2 valeurs est appliqué à un correcteur PID (Proportionnel Intégral et Dérivé) qui calcule la commande appliquée au moteur par l’intermédiaire de l’ampli de puissance. Bien entendu l’asservissement est échantillonné car géré numériquement. Par exemple, la fréquence d’échantillonnage de notre robot 2006 est de 200 Hz soit un contrôle de l’asservissement toutes les 5ms.
Imaginons les 3 figures imposées suivantes :
- Robot à l’arrêt : Il suffit d’appliquer des consignes de position constantes. Le robot est alors immobile et asservi en position, quelle que soit la perturbation qui lui est appliquée (par exemple la poussée d’un robot adverse, avec quand même certaines limites)
- Robot se déplaçant en ligne droite : Il suffit d’appliquer 2 consignes égales en forme de rampe cad proportionnelles au temps. (On ignore pour l’instant les phases d’accélération et de freinage)
- Robot en rotation symétrique : si on ignore également les phases d’accélération et de freinage, il suffit d’appliquer 2 consignes de signes opposés en forme de rampe.
Le rôle du processeur, en fait du programme associé est donc double :
Il doit générer les consignes de position et assurer l’asservissement avec une correction PID. ( toutes les 5 ms).
Jusque là, rien d’original et une solution matérielle classique consiste à utiliser le composant spécialisé LM629 qui permet de décharger le processeur central de cette double tache. Solution qui a le mérite de la simplicité avec toutefois des limites en performance. (Personnellement on n’utilise plus ce composant depuis la disparition des PMI dans le règlement).
Asservissement de position, principe 2 :
Cette année une grande amélioration dans la qualité de notre asservissement résulte de la modification suivante : Les 2 consignes de position sont remplacées par une consigne de distance et une consigne d’orientation conformément au schéma fonctionnel suivant :
asservissement en position : principe 2
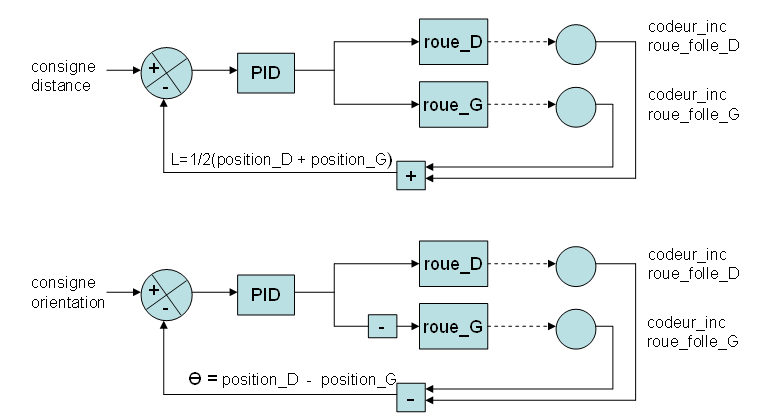
On impose une consigne de distance et une consigne d’orientation au robot
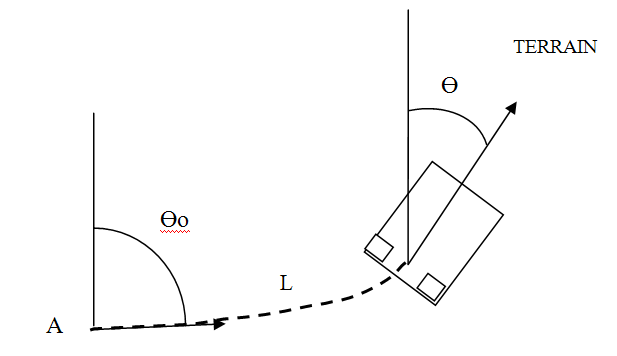
La ligne en pointillé représente la trajectoire curviligne suivie par le robot depuis sa position initiale A
Supposons les conditions initiales suivantes au point A :
- position_D=0 , reset du codeur roue droite
- position_G=0 , reset du codeur roue gauche
- Ө= Өo , orientation initiale du robot
L représente la distance parcourue depuis la position de départ jusqu’à l’instant présent.
L = 1/2.(position_D + position_G)
Ө représente l’orientation du robot à l’instant présent.
Ө = Өo + position_D – position_G
Comparons les 2 principes d’asservissement :
- Principe 1 . Les 2 grandeurs position_D et position_G sont asservies à leurs grandeurs de consigne respectives, consigne_position_D et consigne_position_G.
- Principe 2 . Les 2 grandeurs L et Ө sont asservies à leurs grandeurs de consigne respectives, consigne_distance et consigne_orientation.
Imaginons de nouveau quelques figures imposées mais cette fois avec le principe 2 :
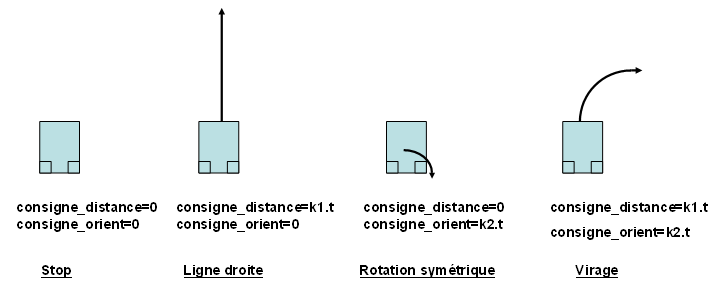
Jusque là, rien de remarquable par rapport au principe 1, si ce n’est la gestion simplifiée des trajectoires curvilignes à rayon constant (Virage). Mais l’intérêt apparaît plus évident dans l’exemple suivant :
On propose de se déplacer du point A vers le point B puis vers C, puis D, …avec une orientation initiale Өo quelconque.
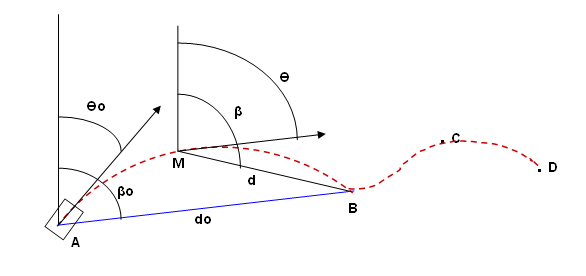
Le robot présente une orientation initiale Өo.
1ère solution : Alignement vers le point B par rotation (βo- Өo)
Puis déplacement rectiligne do suivant le segment de droite AB
2ème solution : Trajectoire curviligne de A vers B (pointillé) obtenue par l’algorithme suivant :
repérer (tant que d non égal à 0)
{
calcul de d et β;
consigne_distante = k1.t;
consigne_orientation = β;
asservissement_vers_valeurs_de_consigne();
}
L’idée est d’asservir à chaque instant d’échantillonnage (point M sur la figure) l’orientation Ө du robot à l’orientation β du point B. Ainsi le robot décrit une trajectoire curviligne en semblant attiré comme par aimantation vers le point B. A noter que la forme de la trajectoire n’est pas imposée. La seule chose qu’on impose au robot est de passer par le point B et ensuite en généralisant de passer par C puis D …
En guise de conclusion et pour introduire la suite :
Cette démarche a permis cette année de slalomer de trou en trou pendant le pillage sans discontinuité de trajectoire et en conservant une vitesse constante (hormis bien sûr les manœuvres d’évitement de l’adversaire). Remarquons que les calculs de la distance restante d et de l’orientation β du point destination supposent que le robot connaisse à tout instant sa position sur le terrain cad les valeurs de ses coordonnées X,Y,Ө. Ce problème actuellement non évoqué, fait l’objet du document suivant « Localisation.doc ».
