Vous pouvez télécharger ce cours au format pdf : Télécharger
Localisation sur le terrain
Connaître sa position sur le terrain, permet à un robot, participant à la coupe Eurobot, d’atteindre un niveau de performance intéressant. Il faut toutefois distinguer la localisation échantillonnée sur le même rythme que l’asservissement (200Hz par exemple) et une localisation ponctuelle qui consiste à recaler le robot à divers moments
stratégiques du match. Le problème du recalage par divers moyens comme par exemple l’utilisation des bordures, de balises
fixes, de lignes tracées sur le terrain ne fait pas l’objet de ce document. On va s’intéresser au problème de la localisation échantillonnée cad le calcul à chaque période d’échantillonnage des coordonnées X,Y,Ө du robot.
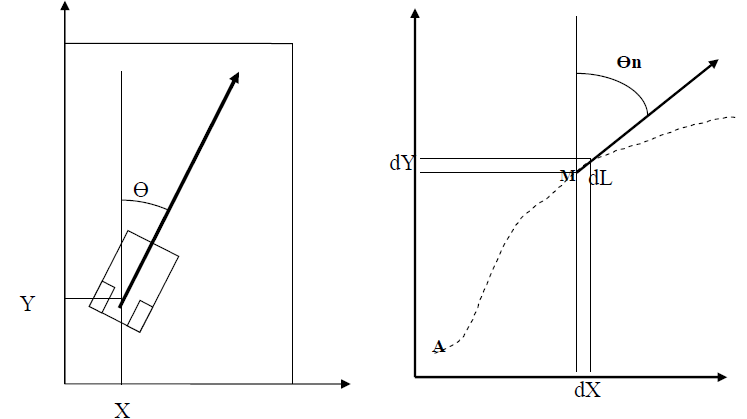
Les coordonnées du robot sont prises au milieu de l’essieu des roues, l’orientation Ө représentant l’angle orienté formé par l’axe longitudinal du robot par rapport à l’axe des Y. (Ө négatif sur la figure). Comme pour le calcul de l’asservissement, on utilise l’information fournie par odomètrie. Mais il faut bien distinguer les 2 problèmes d’asservissement et de localisation. On peut imaginer à l’extrême un robot simplement commandé en boucle ouverte mais capable de pratiquer la localisation (choix à
déconseiller).
Le principe de la localisation peut se résumer simplement :
L’odomètrie permet de calculer la distance parcourue sur la trajectoire, donc la valeur de la vitesse dérivée de la distance. L’odomètrie permettant par ailleurs de connaître l’orientation du robot Ө, cad l’orientation du vecteur vitesse, celui-ci est par conséquent connu (représenté par exemple par le vecteur en trait gras sur la figure droite). Il suffit alors d’intégrer le vecteur vitesse à chaque période d’échantillonnage pour connaître la position du robot. Pas de panique. Nous sommes en numérique. La dérivation s’obtient par une simple soustraction et l’intégration par une simple addition. Représentons en pointillé la trajectoire du robot sur le terrain (figure droite) . Soit Te la période d’échantillonnage. Plaçons nous à l’instant présent n.Te (point M sur la figure). Entre l’instant présent n.Te et l’instant suivant (n+1).Te, le robot s’est déplacé de la distance dL sur sa trajectoire en suivant son orientation Өn.
On rappelle (voir dossier asservissement) que :
Ln=1/2.(position_roue_D + position_roue_G)
Өn= Өo + (position_roue_D – position_roue_G)
Өo représentant l’ orientation initiale du robot (au point A sur la figure).
Par définition la vitesse est égale à la distance parcourue pendant l’unité de temps égale à Te.
Soit :
Vn = dL = Ln+1 – Ln (vitesse à l’instant nTe)
En projetant dL sur les 2 axes :
dX= -Vn .sin(Өn)
dY= Vn .cos(Өn)
En intégrant X et Y :
Xn+1=Xn + dX
Yn+1=Yn + dY
L’algo d’actualisation de X et Y devient aussi simple que ça :
Fonction localisation échantillonnée
{
X=Xo ; // initialisation du robot
Y=Yo ;
Ө= Өo ;
Répéter à chaque Te
{
saisie_codeurs_incrementaux() ;
L=1/2.(position_roue_D + position_roue_G) ;
Ө= Өo + (position_roue_D – position_roue_G) ;
vitesse=L – Lprecedent ; // dérivation
Lprecedent = L ;
deltaX= -vitesse*sin (Ө) ;
deltaY= vitesse*cos(Ө) ;
X=X + deltaX ; //intégration
Y=Y + deltaY ;
}
}
Pour conclure, si le terrain autorise l’odomètrie, celle-ci permet à la fois d’assurer l’asservissement en position des 2 roues du robot et la connaissance de sa position à tout instant (d’échantillonnage). A partir de là tout devient possible…
