Vous pouvez télécharger ce cours au format pdf : Télécharger
Gestion statistique des déplacements trou à trou
Le principe s’applique aussi bien à la dépose des balles, qu’au pillage de celles-ci. Dans les 2 cas, il prend en compte la gestion de l’adversaire et le contournement des totems.
Principe de base :
Afin de simplifier la présentation, on ne tient pas compte pour l’instant des totems et de l’adversaire.
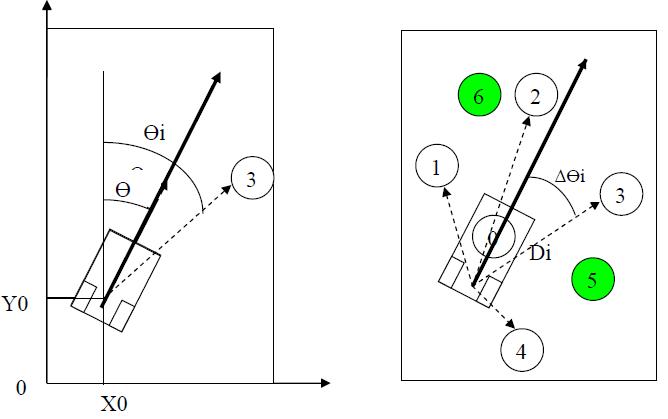
A chaque instant, la position du robot est connue et définie par ses coordonnées X0,Y0 et son orientation Ө. Cette position est déterminée par odomètrie grâce à 2 roues folles de 15 cm de diamètre couplées à 2 codeurs incrémentaux. (Pour ce problème, voir dossier technique complet disponible dans quelques jours). On suppose, à l’instant présent que le robot est positionné sur le trou 0.(figure droite) Le problème évoqué dans ce document est de choisir parmi les trous non encore visités quel va être le trou suivant le plus favorable cad le plus rapidement atteint. Sur l’exemple ci-dessus les trous 5 et 6 déjà visités n’étant pas retenus par l’algo, il reste à choisir parmi les trous 1, 2, 3 et 4. Le robot étant capable de s’asservir à des trajectoires curvilignes, on pourrait imaginer le calcul des temps t1, t2, t3 et t4 mis par le robot pour atteindre chacun de ces trous et retenir le temps minimum. Calcul théoriquement possible mais non réaliste car exigeant une modélisation dynamique du robot avec des temps de calcul incompatibles avec nos processeurs embarqués. Notre solution inspirée de la méthode des moindres carrés est la suivante :
Le robot calcule la distance qui le sépare de chacun des trous d’indice i, non encore
visités :
Di² = (Xi-X0)²+ (Yi-Y0)²
Di distance au trou d’indice i
X0, Y0 coordonnées du robot (centre de l’essieu arrière)
Xi, Yi coordonnées du centre du trou d’indice i
Le robot calcule également l’angle ΔӨi dont il doit tourner pour atteindre chacun de ces points :
ΔӨi = Өi – Ө
Ө, orientation du robot (calculé par odomètrie comme déjà signalé ci-dessus)
Өi, orientation du trou avec :
Өi = arctg (Xi-X0)/(Yi-Y0)
(fonction arctg maison calculée à partir d’un tableau pour des raisons de temps de calcul).
Question : Le robot doit-il privilégier la distance minimum ou la rotation minimum ?
Réponse : Les deux mon capitaine.
C’est là qu’intervient la notion statistique ou empirique (les 2 notions se rejoignent).
On définit une fonction coût :
coût = Di²+ K. ΔӨi²
K étant une constante à optimiser.
Le robot va calculer la fonction coût pour chacun des trous d’indice i (non encore visités) et retenir le trou qui minimise cette fonction. Quant à la constante K, elle est déterminée statistiquement (empiriquement) en se livrant à de nombreux essais de dépose avec des dispositions différentes et en chronométrant la durée totale de la séquence de dépose. (On retient bien sûr la valeur K qui correspond à la séquence de durée minimale). Par exemple, avec notre robot nous avons retenu cette année 2 valeurs :
Une valeur K=3 pour laquelle le robot a plutôt tendance à favoriser les trajectoires tendues (Robot à tempérament FONCEUR) et une valeur K=2 pour laquelle le robot a plutôt tendance à slalomer (Robot à tempérament FOUINEUR). Cette démarche est d’autant plus intéressante qu’elle va permettre d’introduire maintenant la gestion des totems et de l’adversaire, le résultat étant un robot autonome capable d’optimiser ses trajectoires dans n’importe quelle situation. Pour résumer, si on écarte pour l’instant totems et adversaire, l’algo d’une séquence de dépose se présente comme suit :
sequence_depose()
{
va_vers_trou (0) ;
depose_balle( ) ;
répéter tant que (réservoir non vide)
{
i = recherche_indice_trou_suivant( ) ;
va_vers_trou (i) ;
depose_balle( ) ;
}
}
Gestion des totems :
On introduit maintenant les totems dans la recherche du trou suivant. Grâce à un télémètre laser et un simple capteur infra rouge de proximité, la position des totems est connue à l’instant 0 du match.
Le principe de gestion des totems est alors le suivant :
On s’interdit le contournement de totems (Sauf cas spécifique non évoqué pour l’instant). Ainsi après avoir calculé l’indice i du trou suivant le plus favorable, si la trajectoire vers ce trou est supposée rencontrer un totem, on reprend la recherche du trou suivant en éliminant provisoirement cet indice i de la recherche. Ainsi le robot va s’interdire la trajectoire passant par le totem et choisir une trajectoire vers le trou le plus favorable sans contournement.
Comment prévoir que la trajectoire vers le trou suivant va rencontrer un totem ?
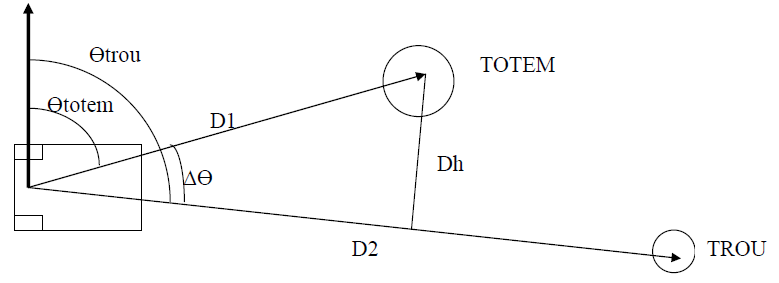
Si D2 < (D1-20cm), aucun risque de rencontrer le totem
Sinon (cas de la figure)
Si Dh > (demi_largeur_robot + rayon_totem + marge_securité), aucun risque
Sinon collision
Evaluation de Dh :
D1 et D2 sont facilement calculés connaissant les coordonnées du robot, du totem et du trou. Il en va de même des orientations du totem Өtotem et du trou Өtrou.
On en déduit :
ΔӨ = Өtotem -Өtrou
Dh = D1.sin(ΔӨ)
L’algo simplifié de dépose avec gestion des totems devient :
sequence_depose( )
{
va_vers_trou (0) ;
depose_balle( ) ;
répéter tant que (réservoir non vide)
{
répéter
{
i = recherche_indice_trou_suivant( ) ;
Si (contournement_totem_pour_indice(i) ==1)
trou[i].accessible=0 ;
Sinon
break ;
}
va_vers_trou(i) ;
depose_balle( ) ;
}
}
Gestion de l’adversaire:
On va introduire maintenant la gestion de l’adversaire :
Deux types de capteurs sont dédiés à cette fonction. Une tourelle infra rouge couplée à la balise embarquée permet de gérer l’adversaire sur les grandes distances. L’info recueillie nous servant pour les grandes décisions
stratégiques devient hors sujet dans cet exposé. Trois capteurs à ultra son dirigés vers l’avant nous permettent de repérer un
adversaire avec risque de collision imminente. Si les capteurs sont validés, le robot stoppe en freinage max, recule de 20 cm et essaie d’échapper en recherchant le trou le plus favorable cad un trou non encore visité mais cette fois situé le plus en arrière
possible pour l’orientation mais le moins loin possible pour la distance (Il s’agit d’éviter l’adversaire en perdant le moins de temps possible)
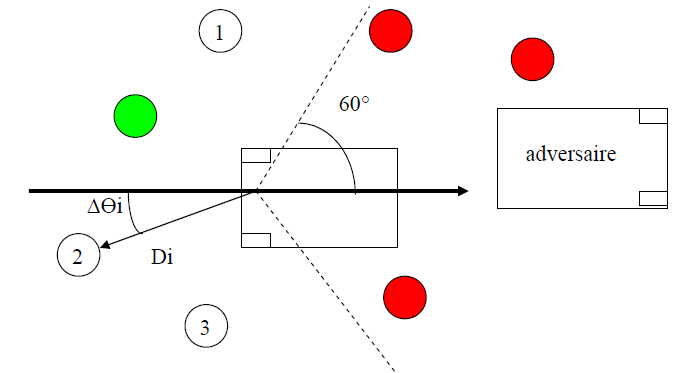
Les trous en rouge sur la figure ci-dessus sont situés à droite de la limite en pointillé, donc considérés comme inaccessibles (car risque de collision) et écartés de la recherche du trou suivant. Le trou en vert a été déjà visité donc également écarté de la recherche. Il s’agit de choisir, dans notre exemple entre les trous 1, 2 et 3.
Là encore, on définit une fonction coût :
coût = Di²+ K. ΔӨi²
et on choisit parmi les trous possibles, celui qui minimise sa fonction coût. Ca deviendra le trou suivant qui doit permettre d’éviter l’adversaire en s’échappant vers l’arrière. On choisit l’échappement vers l’arrière (ΔӨi le plus faible possible) car ne connaissant pas le vecteur vitesse de l’adversaire, celui-ci peut très bien dévier latéralement. Donc statistiquement, le plus sûr pour éviter la collision est de prendre du recul vers l’arrière, (sachant très bien que dans de nombreux cas, ce choix va ouvrir
la porte à l’adversaire).
En guise de conclusion :
L’idée dans cette démarche a été d’éviter un robot de type automate mais au contraire de concevoir un robot qui choisit et optimise ses déplacements face à des situations nombreuses et variées.
L’écriture de la fonction universelle ‘ recherche_indice_trou_suivant( )’ a demandé beaucoup de réflexion ( La présentation dans ce document est incomplète et simplifiée). Mais l’intérêt d’une fonction unique et universelle tient en plusieurs
points :
- Réduction considérable du volume de code (à performances égales).
- Amélioration de la fiabilité car on peut se consacrer à fond sur la mise au point de cette fonction unique (ça semble un point capital !).
- On peut espérer que le robot se sortira de toutes les situations, à la différence d’une gestion automate ou on doit envisager tous les cas possibles (et on oublie toujours le cas qui va se produire au plus mauvais moment cad en situation de match).
- Robot relativement performant car sensé se sortir de toutes les situations en un temps minimum.
- Résultats excitants car on a l’impression d’avoir insufflé à notre robot un semblant de comportement intelligent.
Ce qui n’a pas été abordé dans ce document :
Il ne suffit pas de dire va_vers_trou(i). Encore faut-il écrire la fonction. Mais il s’agit là d’un autre sujet qui consiste à savoir asservir correctement le robot à une trajectoire et évaluer à tout instant sa position sur le terrain. Ces problèmes qui avaient déjà été évoqués dans le dossier 2005 que nous avions mis sur le forum, sont repris avec des nouveautés dans le projet complet 2006 qui devrait sortir prochainement. Laissez nous quelques jours car ya la coupe du monde et le
barbecue des anciens à bichonner…
